Solution

Use trial and error to find the first root:

• $x=1$: $(1)^3-7(1)^2+4(1)+12 = 1-7+4+12 = 10 \neq 0$

$$x=2 \Rightarrow (2)^3-7(2)^2+4(2)+12 = 8-28+8+12= 0$$

So $x=2$ is a root.

Divide the cubic by $x-2$.

$$\begin{align} x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12} \end{align}$$

$$\begin{align} &\;\: x^2\\ x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12}\\ &\;\: x^3-2x^2\\ \end{align}$$

$$\begin{align} &\;\: x^2\\ x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12}\\ &\;\: x^3-2x^2\\ &\;\:\overline{0 -5x^2+4x+12} \end{align}$$

$$\begin{align} &\;\: x^2-5x\\ x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12}\\ &\;\: x^3-2x^2\\ &\;\:\overline{0 -5x^2+4x+12}\\ &\quad\;\; -5x^2+10x \end{align}$$

$$\begin{align} &\;\: x^2-5x\\ x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12}\\ &\;\: x^3-2x^2\\ &\;\:\overline{0 -5x^2+4x+12}\\ &\quad\;\; -5x^2+10x\\ &\qquad \overline{\; 0\:-\:6x\:+\:12} \end{align}$$

$$\begin{align} &\;\: x^2-5x-6\\ x-2&\overline{\big)x^3\!-7x^2\!+4x\!+\!12}\\ &\;\: x^3-2x^2\\ &\;\:\overline{0 -5x^2+4x+12}\\ &\quad\;\; -5x^2+10x\\ &\qquad \overline{\; 0\:-\:6x\:+\:12}\\ &\qquad \quad \; -\:6x \;+\;12\\ &\qquad \qquad \qquad \quad \; \overline{\;0} \end{align}$$

We have already shown that $x=2$ was a root of the cubic equation, so now we must solve $x^2-5x-6=0$ to get the remaining two roots.

By factorising, we have $$x^2 - 5x -6 = (x-6)(x+1)$$

$x=6$ and $x=-1$ are roots of the quadratic, and hence of the cubic equation also.

Therefore, the roots of this cubic are

$$x_1=2, \; x_2=6, \; x_3=-1$$

Here is the graph of $f(x)=x^3-7x^2+4x+12$.

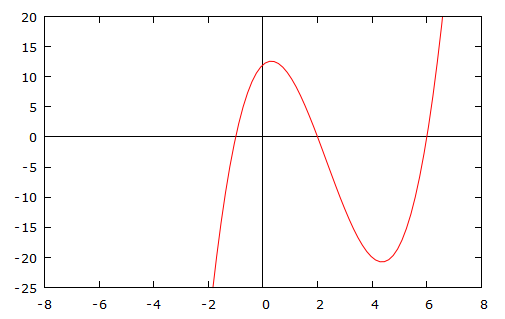
As you can see, it crosses the axis three times, at the points $x=2$, $x=6$ and $x=-1$.

Solution

Use trial and error to find the first root:

$$x = 1 \Rightarrow 2(1)^3+3(1)^2-11(1)-6 = 2+3-11-6 = -12 \neq 0$$

$$x=2 \Rightarrow 2(2)^3+3(2)^2-11(2)-6 = 16+12-22-6= 0$$

So $x=2$ is a root.

Use the polynomial factorisation method to pull out a factor of $x-2$:

$$2x^3+3x^2-11x-6 = 2x^2(x-2)+7x(x-2)+3(x-2) = (x-2)(2x^2 + 7x + 3)$$

Now solve the quadratic $2x^2+7x+3=0$ to find the last two roots.

Using the quadratic formula:

$$\begin{align} x &= \frac{-7 \pm \sqrt{7^2-(4\times2\times3)} }{2\times2}\\ &=\frac{-7 \pm \sqrt{49 - 24} }{4}\\ &=\frac{-7 \pm \sqrt{25} }{4}\\ &=\frac{-7 \pm 5}{4} \end{align}$$

So $x= \dfrac{-7-5}{4} = -3 \; \text{ or } \; x=\dfrac{-7+5}{4} = -\dfrac{1}{2}$

Therefore, the roots of this cubic are

$$x=2, \; x=-3, \; x= -\dfrac{1}{2}$$

Here is the graph of $f(x)=2x^3+3x^2-11x-6$.

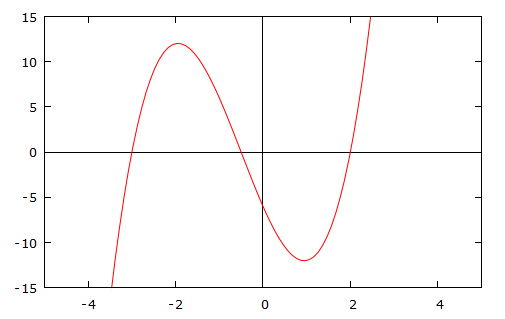
As you can see, it crosses the axis three times, at the points where $x=2$, $x=3$ and $x=-\dfrac{1}{2}$.

Solution

Use trial and error to find the first root:

$$x = 1 \Rightarrow (1)^3-(1)^2-4(1)-6 = 1-1-4-6 = -10 \neq 0$$

$$x = 2 \Rightarrow (2)^3-(2)^2-4(2)-6 = 8-4-8-6= -10 \neq 0$$

$$x = 3 \Rightarrow (3)^3-(3)^2-4(3)-6 = 27-9-12-6= 0$$

So $x=3$ is a root.

Divide the cubic by $(x-3)$:

$$x^3-x^2-4x-6 = x^2(x-3)+2x(x-3)+2(x-3) = (x-3)(x^2 + 2x + 2)$$

The roots of the quadratic $x^2+2x+2$ yield the remaining two roots of the cubic.

We will start by finding the discriminant of the quadratic to see if it has real roots.

We have the values $a=1$, $b=2$ and $c=2$, so the discriminant is $$b^2-4ac = 2^2-(4\times 1\times 2) = 4-8 = -4.$$

The discriminant is negative, so the quadratic has no real roots.

Therefore, this cubic only has one real root, $x=3$.

Here is the graph of $f(x)=x^3-x^2-4x-6$.

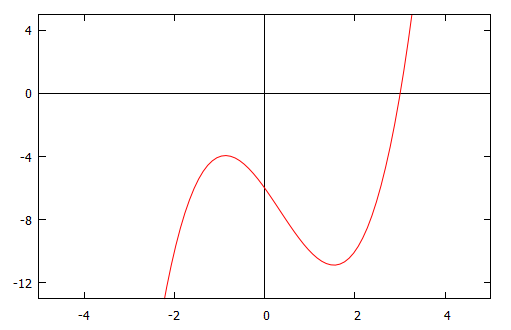
As you can see, it crosses the $x$-axis only once, at the point $x=3$.