Recent research highlights
Vortex reconnections, double reconnections and
rebounds in trapped Bose-Einstein condensates
Reconnections and interactions of filamentary coherent structures play a fundamental role in the dynamics of fluids,
plasmas and nematic liquid crystals. In fluids, vortex reconnections redistribute energy and helicity among the length i
scales and induce fine-scale turbulent mixing. Unlike ordinary fluids where vorticity is a continuous field, in
quantum fluids vorticity is concentrated into discrete (quantized) vortex lines turning vortex reconnections into
isolated events, conceptually easier to study. Here we report experimental and numerical observations of three-dimensional
quantum vortex interactions in a trapped cigar-shaped atomic Bose-Einstein Condensate (BEC). The vortices are generated
by thermall quenching Bose gas (Kibble-Zurek mechanism).
In addition to standard vortex reconnections (already numerically and experimentally observed in homogeneous systems away
from boundaries) we show that double vortex reconnections, vortex rebounds and vortex ejections can also occur
as a consequence of the non-homogeneous, confined nature of the system.
S. Serafini, L. Galantucci, E. Iseni, T. Bienaime, R.N. Bisset,
C.F. Barenghi, F. Dalfovo, G. Lamporesi and G. Ferrari,
Vortex reconnections and rebounds in trapped atomic Bose-Einstein condensates
To be published in Phys Rev X (2017),
(arXiv)
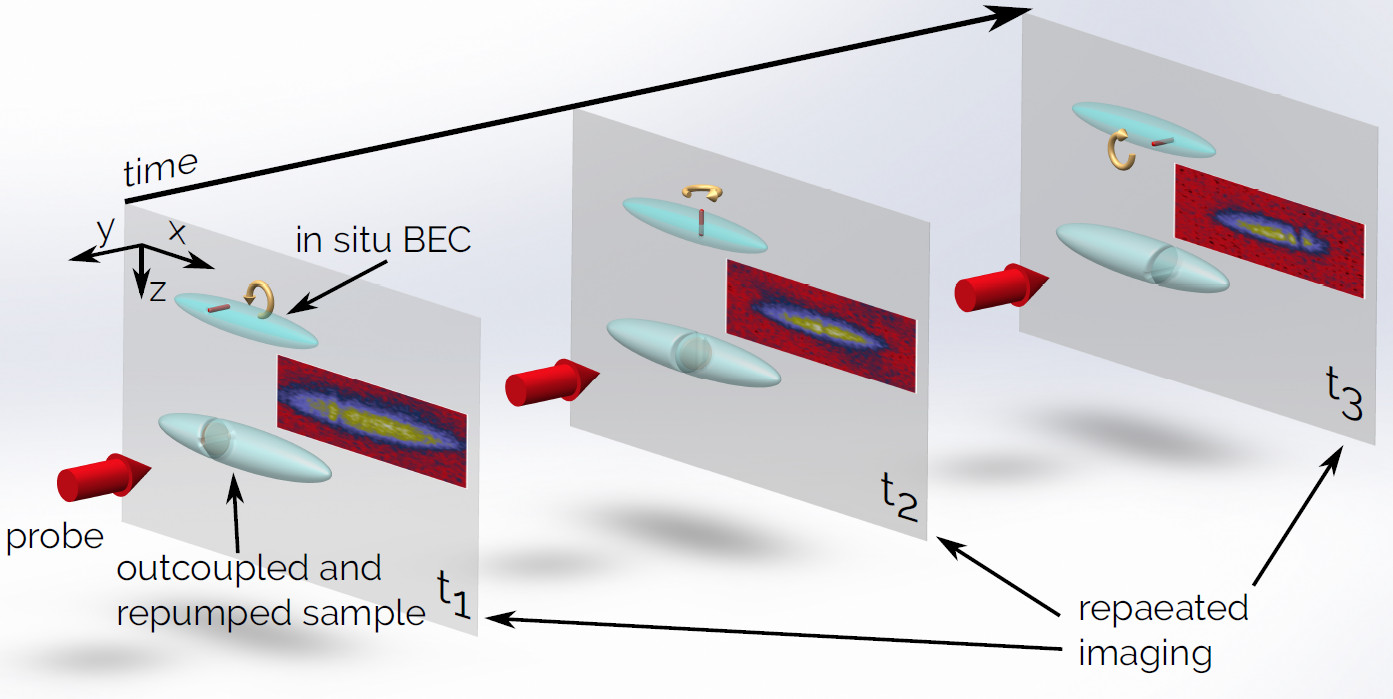
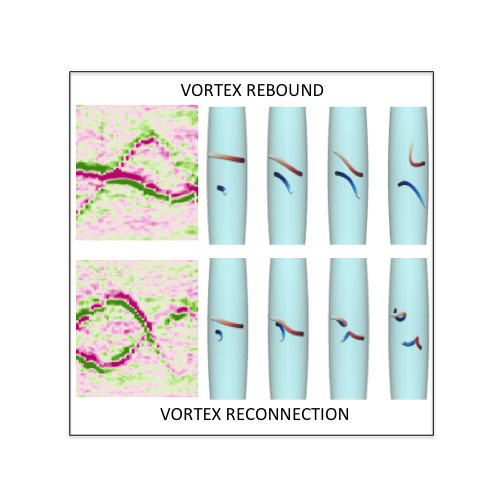
Left: non-destructive technique to image the vortex configuration (by successive outcoupling a small fraction
of atoms) and to determine positions and orientations of the
interacting vortices. Right: vortex rebound (top) and vortex reconnection (bottom). The left panel shows
experimental residuals, the right panels show numerical simulations. In the rebound, the two vortices approach each other,
turn, forming an antiparallel configuration, travel across the condensate, and then move away from each other, without touching.
In the reconnection, the two vortices collide, then part of the first vortex joins the second vortex and viceversa.
Superfluid boundary layer
Vorticity in superfluid helium is constrained to thin vortex lines of fixed circulation and fixed
vortex core size, approximately 0.1 nm. At this scale, the boundaries which contain the liquid helium
cannot be considered smooth. We expect that vortex lines may nucleate from the mountains or valleys
of the surface roughness, or may become pinned. The question of whether vortex lines can slide along
rough a surface has never been tackled before: the implicit assumption has always be that superfluid
helium can slide along boundaries. To find if this is really the case, we have
modeled the superfluid flow of liquid helium over the rough surface of a niobium-titanium (NbTi)
wire (used by Rich Haley and Chris Lawson to experimentally generate turbulence at Lancaster University)
profiled by Atomic Force Microscopy AFM). Numerical simulations of the Gross-Pitaevskii equation have
revealed that the sharpest features on the surface induce vortex nucleation both intrinsically
(due to the raised local fluid velocity) and extrinsically (providing pinning sites to vortex lines
aligned with the flow, which become twisted and spool more vortex lines). Vortex interactions and
reconnections contribute to form a dense turbulent layer of vortices with a nonclassical average velocity
profile which continually sheds small vortex rings into the bulk. We characterize this layer for
various imposed flows. As boundary layers conventionally arise from viscous forces, this result
opens up new insight into the nature of superflows.
GW Stagg, NG Parker, and CF Barenghi,
Superfluid boundary layer
Phys Rev Lett 118 135301 (2017),
(arXiv)
(article)
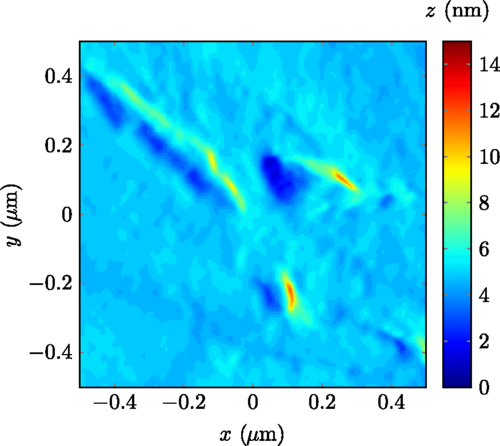
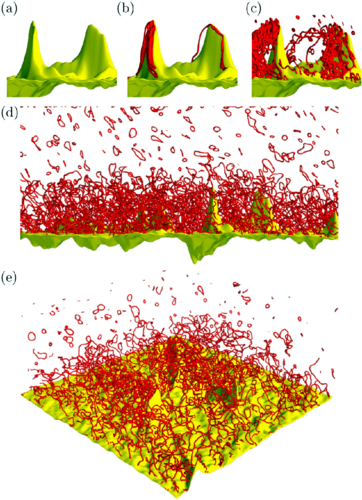
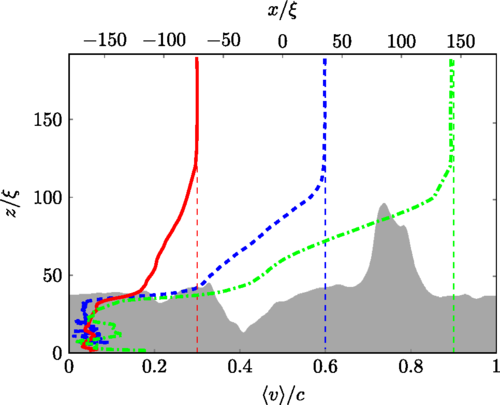
Left: AFM image of a section of the NbTi wire rough surface.
Note the 'mountains' and 'valleys'. Middle:
Vortex nucleation and formation of the turbulent boundary layer
for imposed flow v=0.6c. Isosurface density plots showing the
surface (yellow) and the vortex line (red) in the vicinity of
the two tallest mountains at three different times.
In (c) note three vortex lines which are aligned along the
imposed flow and develop unstable Kelvin waves which will
reconnect and create new vortex loops. (d)and (e) show isosurfaces
of the entire surface in the saturated turbulent regime at
a later time. Note that the turbulent layer extends up to approximately
the height of the tallest mountains; above it there is
a region of small vortex rings. Right: average superfluid velocity
(bottom scale), as a function of height, z (left scale), for v=0.3c
(solid red line), v=0.6c (solid blue line), and v=0.9c
(dot-dashed green line) in the saturated regime.
The grey surface silhouette shows the highest mountain.
Quantum turbulence without energy cascade
Experiments and numerical simulations of turbulent superfluid helium
have established that, at hydrodynamic length scales larger than the
average distance between quantum vortices, the
energy spectrum obeys the same 5/3 Kolmogorov law which is observed
in the homogeneous isotropic turbulence of ordinary fluids. The
importance of the 5/3 law is that it points to the existence of a
Richardson cascade which transfers kinetic energy from
large eddies to small eddies.
However, there is also experimental evidence of quantum turbulent
regimes without Kolmogorov scaling. Why does the
Kolmogorov spectrum fail to form in such regimes?
What is the physical nature of turbulence without energy cascade ?
In this work we describe simple physical mechanisms which prevent the
formation of Kolmogorov scaling in superfluid helium at both high
and low temperatures. Thee first regime, at high temperatures,
is turbulence
generated by a heat flux (thermal counterflow). The second regime,
at low temperatures, is turbulence generated by injecting vortex rings.
CF Barenghi, YA Sergeev, and AW Baggaley,
Regimes of turbulence without an energy cascade'
Nature Scientific Reports 6 35701 (2016),
(arXiv)
(article)
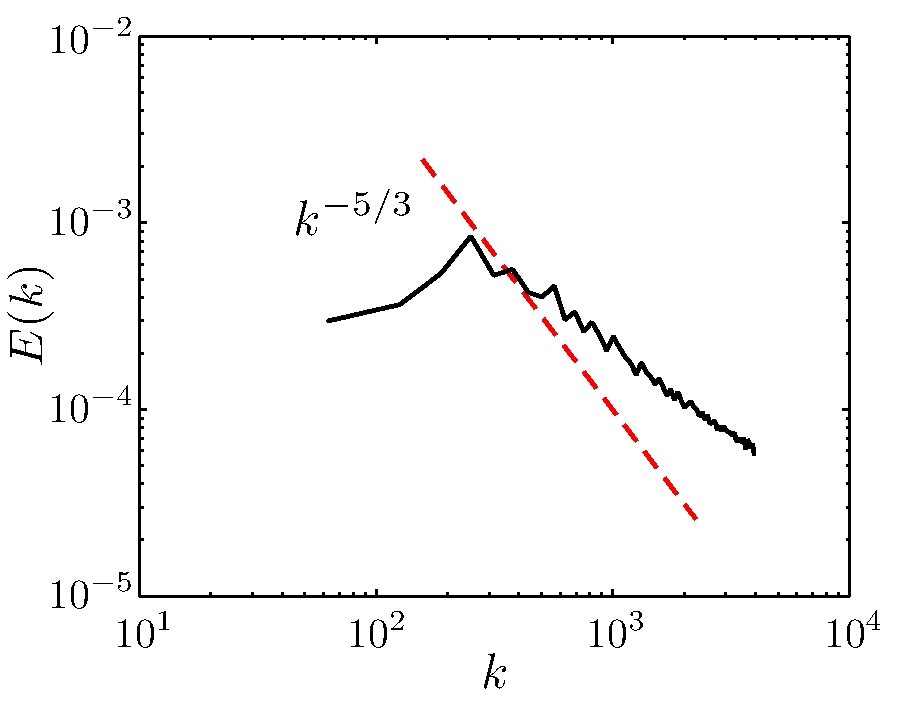
Computed superfluid energy spectrum E(k) vs wavenumber k for thermal
conterflow. Note
that energy is concentrated at intermediate k (not at small k
as in classical turbulence) and, at large k, differs from the
classical k^(-5/3) Kolmogorov scaling (red dashed line).
Leapfrogging vortex rings and Kelvin waves
Two coaxial vortex rings at close distance to each other form
a "leapfrogging" configuration (the vortex which is initially behind shrinks,
speeds up, goes inside the vortex which was initially in front, overtaling it,
then becomes larger and slows down; at this point the process repeats,
without any reconnection, without ending).
This phenomenon has been known since the times of Helmoltz, and has been
recently generalized (DH Wacks, AW Baggaley and CF Barenghi,
Physics of Fluids, 26, 027102, 2012) to configurations
of up to about 100 vortex rings and compared to experiments.
For example, the left figure shows three leapfrogging vortex rings.
Using again parameters suitable for superfluid helium, here we describe a
recurrence phenomena similar to leapfrogging rings
which occurs for two coaxial
straight vortex filaments with a helical perturbation (called Kelvin wave).
The figure
at the right shows a vortex initially inside a helical Kelvin wave;
the inner vortex develops a Kelvin wave of the same wavelenght which
grows in amplitude, so that the inner vortex becomes the outer
vortex, and the process repeats periodically without any reconnection.
Besides superfluids, helical vortices are also important
in viscous flows, where they appear in wakes behind propellers.
Niklas Hietala, Risto Hanninen, Carlo F Barenghi and Hayder Salman,
Leapfrogging Kelvin waves
to appear in Phys Rev Fluids (2016),
(arXiv)
DH Wacks, AW Baggaley and CF Barenghi,
Coherent laminar and turbulent motion of toroidal vortex bundles,
Phys of Fluids, 26 027102 (2012),
(arXiv)
(article)

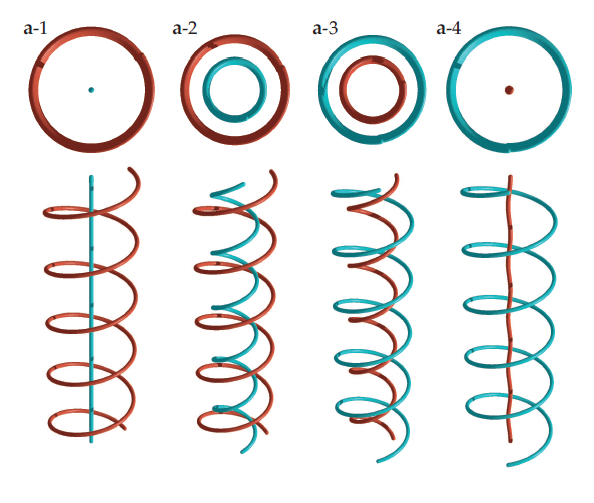
Left: Three leapfrogging vortex rings (Phys Fluids 2012);
notice for example the red vortex which is initially ahead
and which grows in size, slowing down and falling behind the other rings,
and then overtakes them again from the inside.
Right: Leapfrogging Kelvin waves (Phys Rev Fluids to be published), top
and side views. Notice the blue vortex, initially straight and inside the
red vortex with Kelvin wave, which develop a Kelvin wave of the same
wavelength; this Kelvin wave grows in amplitude until the blue vortex
becomes the outer vortex and the red vortex becomes the inner vortex.
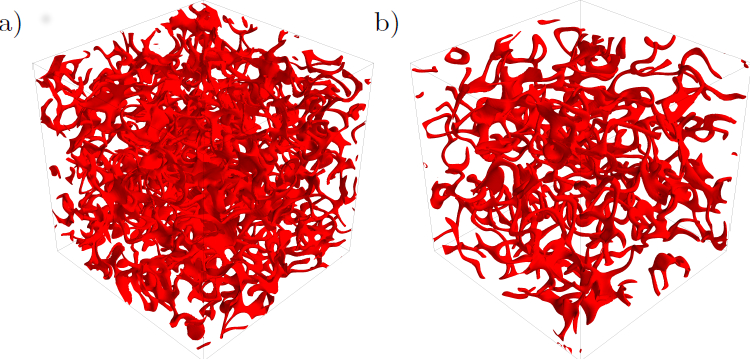
Ultra-quantum turbulence in a quenched homogeneous Bose gas
Using the classical field method, we study numerically the
characteristics and decay of the turbulent tangle of quantum vortices
which is created in the evolution of a Bose gas from highly
nonequilibrium initial conditions. By analysing the vortex line density, the
energy spectrum and the velocity correlation function, we determine
that the turbulence resulting from the thermal quench lacks the
coherent structures and the Kolmogorov scaling (typical of
ordinary turbulence and of turbulent superfluid helium
when driven by grids or propellers). Instead, thermal quench turbulence
has properties akin to a random flow, more similar to another turbulent
regime called ultra-quantum turbulence which has been
observed in superfluid helium.
GW Stagg, NG Parker and CF Barenghi,
Ultra-quantum turbulence in a quenched homogeneous Bose gas
to appear in Phys Rev A (2016)
arXiv
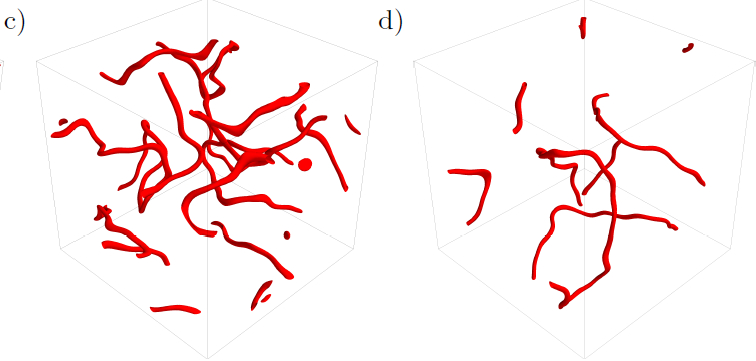
Formation and decay of turbulent tangle of quantum vortices. At t=0 the
occupation number n(k) is uniformly distributed in k-space. Quickly, n(k)
concentrates at low k (large length scales) creating a condensate. Phase
defects organize into a turbulnt tangle of vortices, which slowly decays
to a vortex-free state)
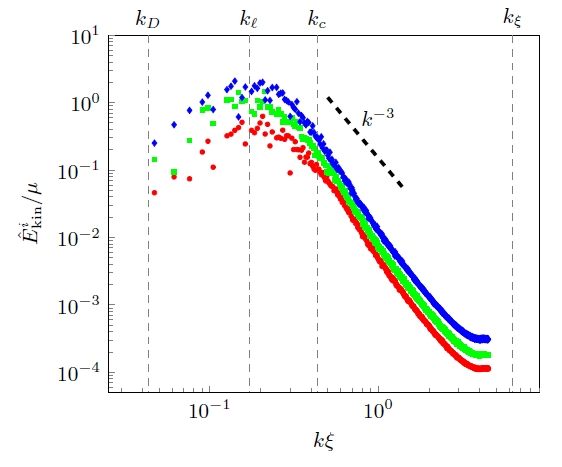
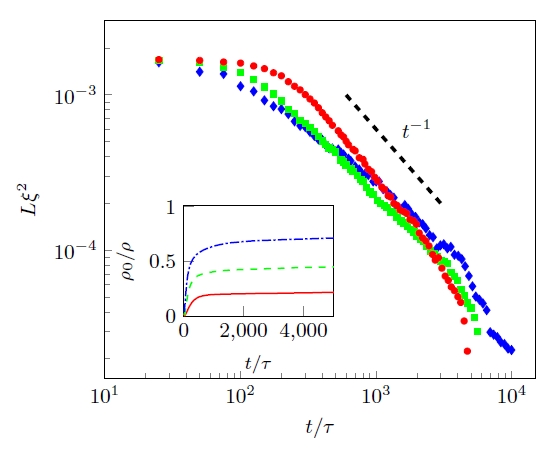
Left: energy spectrum. Note that energy peaks at the intermediate length scales
(rather than the largest length scales (small k). Right: temporal decay
of the vortex line density L ; note that L~t^(-1).
Quantum turbulence in trapped atomic Bose Einstein condensates
Turbulence, the complicated fluid behavior of nonlinear and statistical
nature, arises in many physical systems across various disciplines,
from tiny laboratory scales to geophysical and astrophysical ones.
The notion of turbulence in the quantum world was conceived long ago
by Onsager and Feynman, but the occurrence of turbulence in
ultracold gases has been studied in the laboratory only very recently.
Albeit new as a field, it already offers new paths and perspectives
on the problem of turbulence.
Here we review the general properties of quantum gases at
ultralow temperatures paying particular attention to vortices,
their dynamics and turbulent behavior. We review the recent advances
both from theory and experiment. We highlight the difficulties of
identifying and characterizing turbulence in gaseous Bose-Einstein
condensates compared to ordinary turbulence and turbulence in
superfluid liquid helium and spotlight future directions of research.
MC Tsatsos, PES Tavares, A Cidrim, AR Fritsch, M Caracanhas, FE dos Santos,
CF Barenghi, and VS Bagnato,
Quantum turbulence in trapped atomic Bose-Einstein condensates'
Physics Reports 622 1-52 (2016)
arXiv
article
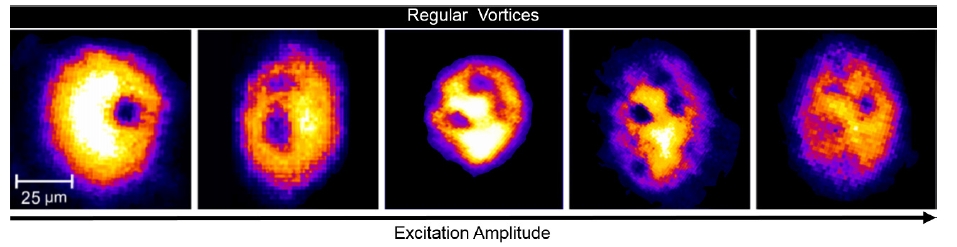
Top: experimental absorption images of
condensates containing 1, 2, 3 and more quantum regular vortices.
Bottom: images of condensates containing turbulent vortices.
Visualizing pure quantum turbulence in superfluid He3
Superfluid He3-B at very low temperatures gives insight into quantum turbulence in its most pure
and fundamental form - a tangle of vortex filaments in a fluid without viscosity which move under
the influence of each vortex on all the others (Euler dynamics) and also reconenct with each other.
At these extreme low tempertures (175 microKelvin) flow visualization is
not trivial: it is based on Andreev scattering of ballistic thermal excitations, a peculiar
scattering in which a quasiparticle is bounced off the velocity field of a quantum vortex, becoming
a quasiholes and (unlike classical reflections) going back along the same direction it arrived
(the same scattering affects incoming quasiholes).
In this work we show the relation between the vortex line density (which characterizes the intensity
of the turbulence) and the Andreev reflectance of the vortex tangle, in the first simulations
of Andreev reflections by a realistic turbulent tangle of vortices. We compare the results with
experiments, probing for the first time the turbulence on length scales smaller than the vortex
separation.
AW Baggaley, V Tsepelin, CF Barenghi, SN Fisher, GR Pickett, YA Sergeev,
and N Suramlishvili,
Visualizing Pure Quantum Turbulence in Superfluid 3He: Andreev Reflection and its Spectral Properties
Phys. Rev. Lett. 115, 015302 (2015)
arXiv
article

2D representation of the reflection coefficient of
thermal excitations incident on a turbulent tangle from one
side of the cell. The vortex lines are shown in yellow, the
regions of high/low Andreev reflectivity are in dark/light/blue.








